Usage generates shape, paths shape the city. Who has never gotten lost in the maze of streets in the medieval center of our cities, sometimes even in our very own city. . . until we find a street map or can ask somebody the way? A map is a representation of the street network, a very effective analogon, showing all possible paths within a city. It is also a drawn image that has intrigued and challenged many architects, urban planners, even artists, and now physicists: our eye perceives an underlying order that organizes this network. But what order, and why?

And what, in fact, is a city? Historical anthropology has shown us temporary and subsequently permanent groupings around markets and seats of power. Ultimately, the city aims to multiply and facilitate both material and symbolic exchanges between individuals. To this end, it brings them closer together and ensures links that will enable them to exchange ideas. We can read this in the permanent traces of paths that are maintained between the locations of each person and of each activity: the routes that make up the urban network. Usage, originally mainly by the pedestrian, rider, or cart, has shaped the form of this network, according to underlying rules that individuals observe when navigating and moving within it.

They have to memorize the usual path(s), find new ones, indicate to other people the path to follow, as well as understand and memorize directions given by another person: which information will be the easiest to remember, the most effective? Inquiries have shown that in an urban fabric with a complex geometry, the path that is described, easily remembered, and actually traveled is the one with the fewest turns, i.e., the fewest changes of route. This is what we call the smallest topological distance between one point in the city and another, between one route in the network and another (each change of route increases the topological distance by one). This travel strategy is used by both pedestrians and taxi drivers (Pailhous 1970).

It is important to talk about route (voie, in French), not street (administrative entity defined by a name). The notion of route that we specifically reconstruct to allow automatic calculation afterward, is continuous, made up of elementary segments (between two intersections), and as perfectly aligned as possible (we choose the smallest angle at each intersection). As in work on collective stampedes, the individual who advances in a given general direction prefers to move through any open space available to them as near as possible to that direction (visibility). We therefore maintain the geometry (the angles formed by the routes between each other) in addition to the topology of the network, which are the essential parameters in human practice. Herein lies the originality of our method: previous approaches to urban road networks overlooked this anthropological reality of the path and the route.

In our ongoing project we rebuild this super network of the city’s effective routes by mapping elementary segments. We thus analyze it through graph theory, a mathematical topological tool that highlights the underlying structural properties: the distribution of route lengths (which follows a Gaussian distribution: “bell-shaped”), of their degree of connectivity to other routes, largely correlated to their “accessibility” (or closeness: the shortest topological distance to all other routes). This yields a very singular result: the geographical distribution of this property, which results from a pure automatic calculation, is rather precisely superimposed on the history of this city, just as much as on inhabitants’ actual practice, according to the readings of urban planners themselves (see Figure 1).

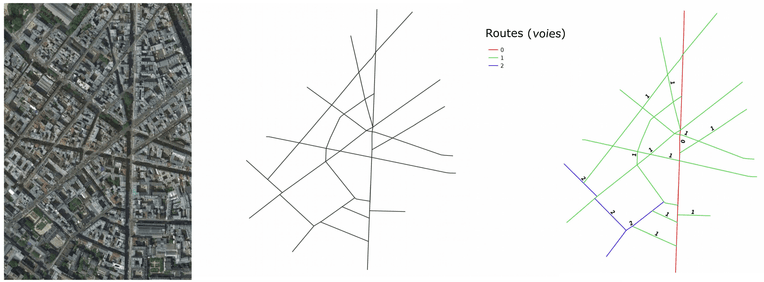
In fact, this is no coincidence but precisely a structural fact. In the history of cities, long routes radiating from the initial basic settlement nucleus ensured the link with other more distant settlement sites. Then, the concentration of the population made this star-shaped initial form more complex, prompting the creation of a new generation of routes that lie perpendicular to existing ones, in 3, 4, 5 iterations. The first routes will therefore remain the longest and best connected to the whole, as long as modern urban planning restructuring operations (we can think of Haussmann’s work) do not modify the path hierarchy.

Our hypothesis, which is undergoing modelization (Bonnin and Douady 2013; Douady et al. 2015), is that the network of routes is a hierarchical network, structured down through generations, each of which has developed on the existing infrastructure of roads and has subdivided the space up to an incompressible limit (at the time due to developments in construction and transport techniques). We trace this development from a neighboring rural space which is neither neutral nor isotropic but already well-structured and subdivided itself, albeit on a different scale, and which is made necessarily accessible in each of its parcels by a network of rural access roads.

Acknowledgments

This essay was translated from French by Stéphane Gros, Kamala Russell, and William F. Stafford Jr., with the help of Bernadette Sellers.